Question

Urn I contains five red chips and four white chips; urn II contains four red and five white chips. Two chips are drawn simultaneously from urn I and placed into urn II. Then a single chip is drawn from urn II. What is the probability that the chip drawn from urn II is white?

Answer 1

To find the probability that the chip drawn from urn II is white, we need to consider the different scenarios and calculate the probability for each of them.

Step-by-step explanation:

To find the probability that the chip drawn from urn II is white, we need to consider the different scenarios. First, there are two chips drawn simultaneously from urn I and placed into urn II. This means that the number of white chips in urn II could change. Let's calculate the probability for each scenario:

• Scenario 1: Both chips drawn from urn I are red. In this case, the number of white chips in urn II remains the same.
• Scenario 2: One chip drawn from urn I is red and the other is white. In this case, the number of white chips in urn II increases by one.
• Scenario 3: Both chips drawn from urn I are white. In this case, the number of white chips in urn II increases by two.

Considering the initial number of chips in each urn and the probabilities of each scenario, we can calculate the overall probability that the chip drawn from urn II is white.

Answer 2

Answer: Our required probability is 0.56.

Step-by-step explanation:

Since we have given that

In urn I :

Number of red chips = 5

Number of white chips = 4

In urn 2 :

Number of red chips = 4

Number of white chips = 5

Two chips are drawn simultaneously from urn I and placed into urn II. Then a single chip is drawn from urn II.

Probability that the chip drawn from urn II is white is given by

P(E₁) =
`(1)/(2)` = P(E₂)

P(W|E₁) =
`(4)/(9)`

P(W|E₂) =
`(5)/(9)`

So, by "Bayes theorem ", we get that

`P(E_2|W)=(0.5* (5)/(9))/(0.5* (4)/(9)+0.5* (5)/(9))\\\\P(E_2|W)=(5)/(9)=0.56`

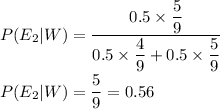
Hence, our required probability is 0.56.