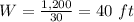Question

Two equal rectangular lots are enclosed by fencing the perimeter of a rectangular lot and then putting a fence across its middle. If each lot is to contain 1200 square feet, what is the minimum amount of fence needed to enclose the lots (include the fence across the middle)?

Answer 1

The minimum amount of fence (minimum perimeter) is 240 feet

Explanation:

see the attached figure to better understand the problem

Let

x ----> the length of one rectangular lot

y ----> the width of one rectangular lot

we know that

The area of the two rectangular lots is equal to

`A=LW+LW`

`A=2(1,200)=2,400\ ft^2`

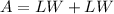
so

`2,400=2LW`

`1,200=LW` ----->
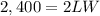
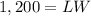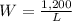`W=(1,200)/(L)` -----> equation A

The perimeter of the two rectangular lots is equal to

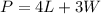`P=4L+3W` ----> equation B

substitute equation A in equation B

`P=4L+(3)(1,200)/(L)`

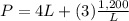
Using a graphing tool

Find out the minimum (vertex) of the function

The minimum is the point (30,240)

see the attached figure

therefore

The minimum amount of fence (minimum perimeter) is 240 feet

The length is
`L=30\ ft`

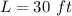
The width is
`W=(1,200)/(30)=40\ ft`