Question

Which set of ordered pairs could be generated by an exponential function?

(1, 1), (2, one-half), (3, one-third), (4, one-fourth)

(1, 1), (2, one-fourth), (3, one-ninth), (4, one-sixteenth)

(1, one-half), (2, one-fourth), (3, one-eighth), (4, one-sixteenth)

(1, one-half), (2, one-fourth), (3, one-sixth), (4, one-eighth)

Answer 1

C.(1,one-half),(2,one-fourth),(3,one-eight),(4,one-sixteenth)

Explanation:

We have to find the set of ordered pair which could be generated by an exponential function.

We know that the range of exponential function is in geometric progression.

When the sequence is geometric then the ratio of consecutive two term is constant.

In first option

Let
`a_1=1,a_2=(1)/(2),a_3=(1)/(3),a_4=(1)/(4)`

`(a_2)/(a_1)=(1)/(2),(a_3)/(a_2)=((1)/(3))/((1)/(2))=(2)/(3)`

`(a_2)/(a_1)\\eq (a_3)/(a_2)`

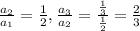
It is not in G.P.

Hence, it is not the set of ordered pairs which could be generated by an exponential function.

In second function

`a_1=1,a_2=(1)/(4),a_3=(1)/(9),a_4=(1)/(16)`

`(a_2)/(a_1)=(1)/(4)`

`(a_3)/(a_2)=((1)/(9))/((1)/(4))=(4)/(9)`

`(1)/(4)\\eq (4)/(9)`

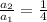
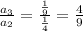
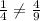
It is not in G.P

Hence, it is not the set of ordered pairs which could be generated by an exponential function.

In III option

`a_1=(1)/(2),a_2=(1)/(4),a_3=(1)/(8),a_4=(1)/(16)`

`(a_2)/(a_1)=((1)/(4))/((1)/(2))=(1)/(2)`

`(a_3)/(a_2)=((1)/(8))/((1)/(4))=(1)/(2)`

`(a_4)/(a_3)=((1)/(16))/((1)/(8))`
`=(1)/(2)`

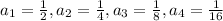
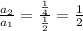
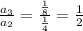
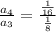
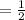
It is in G.P

Hence, it is the set of ordered pairs which could be generated by an exponential function.

In IV option

`a_1=(1)/(2),a_2=(1)/(4),a_3=(1)/(6),a_4=(1)/(8)`

`(a_2)/(a_1)=((1)/(4))/((1)/(2))=(1)/(2)`

`(a_3)/(a_2)=((1)/(6))/((1)/(4))=(2)/(3)`

`(a_2)/(a_1)\\eq (a_3)/(a_2)`

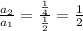
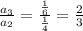
It is not in G.P

Hence, it is not the set of ordered pairs which could be generated by an exponential function.

Answer 2

The correct option is C)
`(1, (1)/(2)), (2, (1)/(4) ), (3,(1)/(8) ), (4,(1)/(16))`

Explanation:

Consider the provided ordered pairs.

The function will be exponential function if the ratio of y value remains the same.

Consider the option

Option A:
`(1, 1), (2, (1)/(4) ), (3,(1)/(3) ), (4,(1)/(4) )`

The ratio of 1/4 and 1 is 1/4 but the ratio of 1/3 and 1/4 is not 1/4.

Therefore, option A is incorrect.

Option B:
`(1, 1), (2, (1)/(4) ), (3,(1)/(9) ), (4,(1)/(16))`

The ratio of 1/4 and 1 is 1/4 but the ratio of 1/9 and 1/4 is not 1/4.

Therefore, option B is incorrect.

Option C:
`(1, (1)/(2)), (2, (1)/(4) ), (3,(1)/(8) ), (4,(1)/(16))`

The ratio of 1/4 and 1/2 is 1/2, the ratio of 1/8 and 1/4 is 1/2

Similarly the ratio of 1/16 and 1/8 is 1/2,

Therefore, option C is correct.

Option D:
`(1, (1)/(2)), (2, (1)/(4) ), (3,(1)/(6) ), (4,(1)/(8))`

The ratio of 1/4 and 1/2 is 1/4 but the ratio of 1/6 and 1/4 is not 1/4.

Therefore, option D is incorrect.