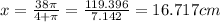Answer:16.71 cm
Explanation:
Given
Length of wire L=38 cm
One piece is bent in the form of square and another in the form of circle
let x be the length of circle
therefore length of square side
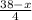
A=total area of square and circle
radius of circle
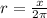
area of circle
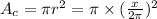
Area of square
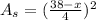

To get the minimum value of A we get
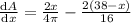
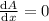
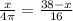
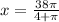
Therefore circumference of circle