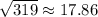Answer:
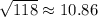
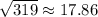
Explanation:
Consider the provided number.
We need to find the approximate value of
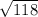 to the nearest hundredth.
to the nearest hundredth.
First find two perfect squares that the irrational number falls between.
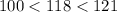
118 is lying between 100 and 121, therefore the square root value of 118 will be somewhere between 10 and 11.
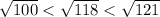

118 is closer to 121 as compare to 100.
Therefore,
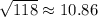
Consider the number
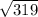
First find two perfect squares that the irrational number falls between.
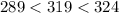
319 is lying between 289 and 324, therefore the square root value of 319 will be somewhere between 17 and 18.


319 is closer to 324 as compare to 289.
Therefore,