Question

Which statement about the end behavior of the logarithmic function f(x) = log(x + 3) – 2 is true?

A.
As x decreases, y moves toward the vertical asymptote at x = -3.
B.
As x decreases, y moves toward the vertical asymptote at x = -1.
C.
As x increases, y moves toward negative infinity.
D.
As x decreases, y moves toward positive infinity.

Answer 1

answer A is correct

Explanation:

Answer 2

Option A is correct.

Explanation:

Let us graph the function
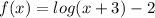`f(x) = log(x + 3)-2` and analyze it.

The graph has one asymptote: the vertical
`x=-3`. With this information, let us analyze each of the options one by one.

Option A: As x decreases, y moves toward the vertical asymptote at x = -3.

This is true because as we move down along the x-axis to the left we meet the vertical asymptote
`x=-3`.

Option B: As x decreases, y moves toward the vertical asymptote at
`x=-1`.

This is incorrect since the vertical asymptote is not located at
`x=-1`

Option C: As x increases, y moves toward negative infinity.

No this is incorrect. As x increases, y moves towards positive infinity.

Option D: As x decreases, y moves toward positive infinity.

No this is incorrect. As x decreases, y moves towards negative infinity.

Thus only option A is correct.