Answer:
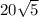
Step-by-step explanation:
According to the question
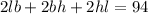
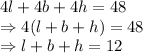
Length of the diagonal is given by
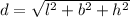
This can be also written as

The length of one diagonal is
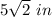
As there are 4 diagonals the sum of the lengths of the prism is
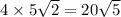
With the given information the exact dimensions of the prism cannot be determined as the two equations cannot be solved and trigonometry can also be not used.