Question

Please Help.
Match the reasons to the statements given.

Answer 1

1. Given

2. Diagonals of a parallelogram bisect each other.

3. Vertical angles are equal.

4. Definition of parallelogram.

5. If lines parallel, then alternate interior angles are equal.

6. ASA

7. CPCTE

Explanation:

Statement 1:

The first statement is a parallelogram ABCD, which is already given in the question. So, reason 1 is: Given.

Statement 2:

BT and TD are equal because for a parallelogram, its diagonal bisect each other. Here, BD and AC are the diagonals of parallelogram ABCD. So, the diagonals bisect each other at T. Hence,
`BT = TD`

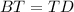
Statement 3:

Angles 1 and 2 is a pair of vertical angles. A pair of vertical angles are always equal to each other.

Statement 4:

A parallelogram is a quadrilateral whose opposite sides are parallel and equal. Hence,
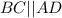`BC ||AD` is because of the definition of a parallelogram.

Statement 5:

Angles 3 and 4 is a pair of alternate interior angles. If two lines are parallel, then the alternate interior angles are always equal.

Statement 6:

The triangles BET and DFT are now congruent because:

i.Angle-
`\angle1=\angle2`

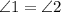
ii. Side -
`BT = TD`

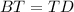
iii. Angle -
`\angle3=\angle4`

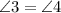
Therefore, by ASA postulate the two triangles are congruent.

Statement 7:

As the two triangles are congruent, then their corresponding parts are also equal.

So, by CPCTE,
`ET=FT`