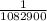Question

If you are dealt five cards from a shuffled deck of 52 cards find the probability of getting three queens and two kings

Answer 1

Explanation:

its .0009234%

I just took the test and this was the answer, I dare you to try it, cuz its right.

Answer 2

The probability of getting three queens and two kings is
`(1)/(1082900)`

Solution:

Given that , you are dealt five cards from a shuffled deck of 52 cards

We have to find the probability of getting three queens and two kings

Now, we know that, in a deck of 52 cards, we will have 4 queens and 4 kings.

`\text { probability of an event }=\frac{\text { favarable possibilities }}{\text { number of possibilities }}`

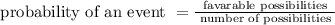
Probability of first queen:

`\text { Probability for } 1^{\text {st }} \text { queen }=(4)/(52)=(1)/(13)`

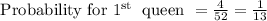
Probability of second queen:

`\text { Plobability for } 2^{\text {nd }} \text { queen }=(3)/(51)=(1)/(17)`

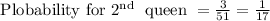
Here we used 3 for favourable outcome, since we already drew 1 queen out of 4

And now number of outcomes = 52 – 1 = 51

Probability of third queen:

Similarly here favorable outcome = 2, since we already drew 2 queen out of 4

And now number of outcomes = 51 – 1 = 50

`\text { Probability of } 3^{\text {rd }} \text { queen }=(2)/(50)=(1)/(25)`

Probability for first king:

Here kings are 4, but overall cards are 49 as 3 queens are drawn

`\text { probability for } 1^{\text {st }} \text { king }=(4)/(49)`

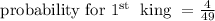
Probability for second king:

Here, kings are 3 and overall cards are 48 as 3 queens and 1 king are drawn

`\text { probability of } 2^{\text {nd }} \text { king }=(3)/(48)=(1)/(16)`

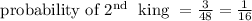
And, finally the overall probability to get 3 queens and 2 kings is:

`=(1)/(13) * (1)/(17) * (1)/(25) * (4)/(49) * (1)/(16)=(4)/(4331600)=(1)/(1082900)`

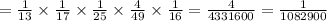
Hence, the probability is
`(1)/(1082900)`