Question

Suppose a life insurance company sells a $240,000 one year term life insurance policy to a 25-year old female for $210. The probability that the female survives the year is .999592. Compute the expected value of this policy to the insurance company. I thought I would start with x value of 1 - 12, but I'm lost on what my P(X=x) value will be. I can do these when I'm shown a chart, however I'm lost when asked to do them from a story problem... An example would be appreciated. Thank you in advance

Answer 1

$112.08 every year.

Explanation:

Let's suppose a game in which we bet a certain amount of money ''A'' to a certain result and the probability of that result is ''p''. If the prize that we get is ''P'' therefore the expected value of gain is :

`E=p(P-A)+(1-p)(-A)=pP-A`

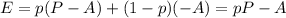
Now,let's suppose that the female is ''betting on her death'' ⇒

P(she survives) = 0.999592

P(she doesn't survive) = 1 - 0.999592=
`4.08(10^(-4))`

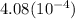
E(25-year old female) =
`4.08(10^(-4)).(240000)-210=-112.08`

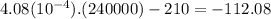
The negative sign of E is important.It means that every year the 25-year old female will lose $112.08.

Therefore, the expected value of this policy to the insurance company is $112.08 every year.