Question

. Using your knowledge of circular (centripetal) motion, derive an equation for the radius r of the circular path that electrons follow in terms of the magnetic field B, the electrons' velocity v, charge e, and mass m. You may assume that the electrons move at right angles to the magnetic field.

2. Recall from electrostatics, that an electron obtains kinetic energy when accelerated across a potential difference V. Since we can directly measure the accelerating voltage V in this expierment, but not the electrons' velocity v, replace velocity in your previous equation with an expression containing voltage. The electron starts at rest. Now solve this equation for e/m.

You should obtain e/m = 2V/(B^2)(r^2)

3. The magnetic field on the axis of a circular current loop a distance z away is given by

B = mu I R^2 / 2(R^2 + z^2)^ (3/2)

where R is the radius of the loops and I is the current. Using this result , calculate the magnetic field at the midpoint along the axis between the centers of the two current loops that make up the Helmholtz coils, in terms of their number of turns N, current I, and raidus R.Helmholtz coils are separated by a distance equal to their raidus R. You should obtain:

|B| = (4/5)^(3/2) *mu *NI/R = 9.0 x 10^-7 NI/R

where B is magnetic field in tesla, I is in current in amps, N is number of turns in each coil, and R is the radius of the coils in meters

Answer 1

Step-by-step explanation:

Magnetic field creates a force perpendicular to a moving charge in its field which is equal to Bev where B is magnetic field , e is amount of charge on the moving charge and v is the velocity of charge particle .

This force provides centripetal force for creation of circular motion. If r be the radius of the circular path

Bev = mv² / r

r = mv / Be

2 ) If an electron is accelerated by an electric field created by potential difference V then electric field

= V / d where d is distance between two points having potential difference v .

force on charged particle

electric field x charge

= V /d x e

work done by field

= force x distance

= V /d x e x d

V e

This is equal to kinetic energy created

V e = 1/2 mv²

= 1/2 m (r²B²e² / m² )

V = r²B²e/ 2 m

e / m = 2 V/ r²B²

3 )

B =
`(\mu* I* R^2)/(2(R^2+Z^2)^(3)/(2) )`

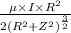
In Helmholtz coils , distance between coil is equal to R so Z = R/2

B =
`(\mu* I* R^2)/(2(R^2+(R^2)/(4) )^(3)/(2) )`

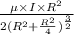
For N turns of coil and total field due to two coils

B =
`(\mu* I* N)/(R*((5)/(4))^(3)/(2)  )`

=
`(\mu* I* N)/(R)* ((4)/(5))^(3)/(2)`

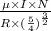
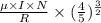
= 9.0 x 10^-7 NI/R