Question

A 4.0-m-diameter playground merry-go-round, with a moment of inertia of

500kg?m2 is freely rotating with an angular velocity of 2.0rad/s . Ryan, whose mass is 70kg , runs on the ground around the outer edge of the merry-go-round in the opposite direction to its rotation. Still moving, he jumps directly onto the rim of the merry-go-round, bringing it (and himself) to a halt. How fast was Ryan running when he jumped on?

Answer 1

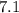`7.1` ms⁻¹

Step-by-step explanation:

`d` = diameter of merry-go-round = 4 m

`r` = radius of merry-go-round =
`(d)/(2)` =
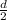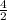`(4)/(2)` = 2 m

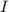`I` = moment of inertia = 500 kgm²

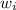`w_(i)` = angular velocity of merry-go-round before ryan jumps = 2.0 rad/s

`w_(f)` = angular velocity of merry-go-round after ryan jumps = 0 rad/s

`v` = velocity of ryan before jumping onto the merry-go-round

`m` = mass of ryan = 70 kg

Using conservation of angular momentum

`Iw_(i) - m v r = (I + mr^(2))w_(f)`

`(500)(2.0) - (70) v (2) = (I + mr^(2))(0)`

`1000 = 140 v`

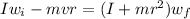
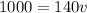
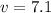`v = 7.1` ms⁻¹