Question

A satellite system consists of n components and functions on any given day if at least k of the n components function on that day. On a rainy day, each of the components independently functions with probability p₁, whereas on a dry day, each independently functions with probability p₂. If the probability of rain tomorrow is α, what is the probability that the satellite system will function?

Answer 1

`(1 - \sum_(j = 0)^(k-1) {n \choose j} * {p_1}^j * (1-p_1)^(n-j)) * a + (1 - \sum_(j=0)^(k-1) {n \choose j} * {p_2}^j * (1-p_2)^(n-j)) * (1-a)`

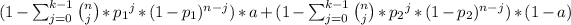
Explanation:

We will call C the number of components that will function tomorrow. R is the event 'tomorrow rains', and D is the event 'tomorrow is a dry day'. The satellite system will work if
`C \geq k`.

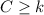We can calculate the probability of the event
`\textbf{textit{C \geq k}}` dividing in 2 cases, depending on if it rains tomorrow (R), of if is a dry day (D). According to the theorem of total probability, we have this formula

`P(C \gek k) = P(C \geq k | R) * P(R) + P(C \geq k | D) * P(D)`

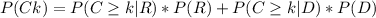
Since D is the complementary event of R, we have
`P(D) = 1- P(R) = 1-a`

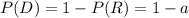
Note that if we assume that it will rain (or not) tomorrow, then C is a random variable of binomial distribution with parameters n and
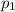`p_1` (or
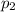`p_2`). To calculate the probability of C being greater than k, we can take probability of the complementary event, in other words, the probability of the event 'C is any j with j between 0 and k-1' and substract it from 1. Therefore

• 
  `P(C \geq k | R) = 1 - \sum_(j = 0)^(k-1) {n \choose j} * {p_1}^j * (1-p_1)^(n-j)`
• 
  `P(C \geq k |D) = 1 - \sum_(j=0)^(k-1) {n \choose j} * {p_2}^j * (1-p_2)^(n-j)`

Using this calculations, we can conclude that

`P(C \geq k) = P(C \geq k |R) * P(R) + P(C \geq k |D) * P(D) \\ = (1 - \sum_(j = 0)^(k-1) {n \choose j} * {p_1}^j * (1-p_1)^(n-j)) * a + (1 - \sum_(j=0)^(k-1) {n \choose j} * {p_2}^j * (1-p_2)^(n-j)) * (1-a)`

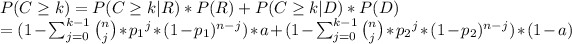
I hope it helps you!