Question

I need this quick please help!!! 3x−1/5 = x+1/3

Answer 1

For this case we must solve the following equation:

`3x- \frac {1} {5} = x + \frac {1} {3}`

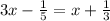
Subtracting "x" from both sides of the equation we have:

`3x-x- \frac {1} {5} = \frac {1} {3}\\2x- \frac {1} {5} = \frac {1} {3}`

Adding
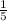`\frac {1} {5}`to both sides of the equation we have:

`2x = \frac {1} {3} + \frac {1} {5}\\2x = \frac {5 + 3} {15}\\2x = \frac {8} {15}`

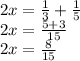
We divide between 2 on both sides of the equation:

`x = \frac {\frac {8} {15}} {2}\\x = \frac {8} {15 * 2}\\x = \frac {8} {30}\\x = \frac {4} {15}`

Thus, the solution of the equation is:

`x = \frac {4} {15}`

Answer:

`x = \frac {4} {15}`