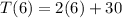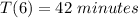Answer:
Part a)
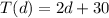
Part b)
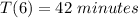
Explanation:
Part a) Write an equation for T (d)
Let
d ----> the number of days
T ---> the time in minutes of the treadmill
we know that
The linear equation in slope intercept form is equal to
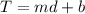
where
m is the slope or unit rate
b is the y-intercept or initial value
In this problem we have
The slope or unit rate is
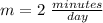
The y-intercept or initial value is
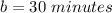
substitute
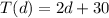
Part b) Find T (6), the minutes he will spend on the treadmill on day 6
For d=6
substitute in the equation and solve for T