Question

A storage shed is to be built in the shape of a box with a square base. It is to have a volume of 686 cubic feet. The concrete for the base costs $8 per square foot, the Material for the roof costs $6 per square foot, and the material for the sides costs $3.50 per square foot. Find the dimensions of the most economical shed.

The length of the's base is X ft

The height of the shed is X ft

Answer 1

(8.44 ft. × 8.44 ft × 9.63 ft.)

Explanation:

A storage shed has the volume = 686 cubic feet.

686 = x²h ----------------(1)

Let the length of square base = x ft

and height of the shed = h ft

Area of concrete base = x² ft²

Cost to build the base = 8x² [since cost to build the square base = $8 per square feet]

Area of the sides of the shed = 4xh

Cost to build the sides = 4xh (3.50) [since cost to build the sides = $3.50 per square ft]

C = 14xh

Total cost = 8x² + 14xh

(C) = 8x² + (14x) ×
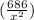`((686)/(x^2))` = 8x² +
`((9604)/(x))`

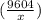
To minimize the cost we will take the derivative of c and equate it to 0.

`(dc)/(dx)=16x-(9604)/(x^2)=0`

`16x = (9604)/(x^2)`

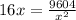
16x³ = 9604

x³ =
`(9604)/(16)`

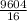
x³ = 600.25

x = 8.44 ft.

For x = 8.44

686 = (8.44)² h

h =
`(686)/((8.44)^2)`

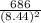
= 9.63 ft

Therefore, for the minimum cost, dimension of the shed should be (8.44 ft. × 8.44 ft × 9.63 ft.)