The quadratic factors of the given expression are (3x + 5) and (5x + 9).
SOLUTION:
Given, quadratic equation is 15x squared + 52x + 45
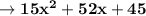
We have to find the quadratic factors for the given quadratic expression.
Now, let us factorize the given expression.

Hence, the quadratic factors are (3x + 5) and (5x + 9).
Steps to factorise quadratic equation:
With the quadratic equation in this form:
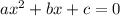
- Step 1: Find two numbers that multiply to give ac (in other words a times c), and add to give b.
- Step 2: Rewrite the middle with those numbers
- Step 3: Factor the first two and last two terms separately
- Step 4: If we've done this correctly, our two new terms should have a clearly visible common factor.