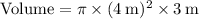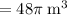Answer:
3.3.1
A cylinder has a circular base.
3.3.2
As cylinders have circular bases, the formula for the area of the base of a cylinder should be the same as the formula for the area of a circle:
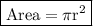 .
.
3.3.3
To find the volume of a cylinder, we can imagine stacking multiple circles on top of each other so that the height of the structure increases, and the shape becomes a cylinder.
This means that the volume of a cylinder is simply the area of the base circle multiplied by the height (h) of the cylinder.
∴
 .
.
3.3.4
We can use the above formula to calculate the volume of the given cylinder, where:
• r =
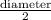 =
=
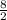 = 4 m
= 4 m
• h = 3 m
∴