Answer:
0.0137
Explanation:
Let X be the random variable that measures the number of incoming calls every ten minutes.
If the incoming calls to the system are Poisson distributed with a mean equal to 5 every 10 minutes, then the probability that there are k incoming calls in 10 minutes is
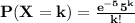
If the phone-answering system is capable of handling ten calls every 10 minutes, we want to find
P(X>10), or the equivalent 1 - P(X≤ 10).
But
1 - P(X≤ 10)= 1 -(P(X=0)+P(X=1)+...+P(X=10)) =
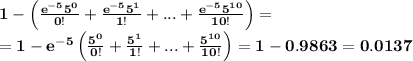
So, the probability that in a 10-minute period more calls will arrive than the system can handle is 0.0137