Question

Write a balanced equation for the combustion of C7H16(l) (heptane) -- i.e. its reaction with O2(g) forming the products CO2(g) and H2O(l). Given the following standard heats of formation: ΔHf° of CO2(g) is -393.5 kJ/mol ΔHf° of H2O(l) is -286 kJ/mol ΔHf° of C7H16(l) is -187.8 kJ/mol What is the standard heat of reaction (ΔH°) for the combustion reaction of C7H16(l)? -4854.7 kJ Calculate the difference, ΔH-ΔE=Δ(PV) for the combustion reaction of 1 mole of heptane. (Assume standard state conditions and 298 K for all reactants and products.)

Answer 1

The standard enthalpy of reaction = -4854.7kJ

The difference: ΔH-ΔE = Δ(PV) = Δn.R.T = 9910.288 J ≈ 9.91 kJ

Step-by-step explanation:

The balanced chemical equation for the combustion of heptane:

C₇H₁₆ (l) + 11 O₂ (g) → 7 CO₂ (g) + 8 H₂O (l)

Given: The standard enthalpy of formation (
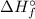`\Delta H _(f)^(\circ )`) for: C₇H₁₆ (l) = -187.8 kJ/mol, O₂ (g) = 0 kJ/mol, CO₂ (g) = -393.5 kJ/mol, H₂O (l) = -286 kJ/mol

To calculate the standard enthalpy of reaction (
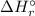`\Delta H _(r)^(\circ )`) can be calculated by the Hess's law:

`\Delta H _(r)^(\circ ) = \left [\sum \\u \cdot\Delta H _(f)^(\circ )(products)  \right ] - \left [\sum \\u\cdot\Delta H _(f)^(\circ )(reactants)  \right ]`

Here,
`\\u` is the stoichiometric coefficient

⇒
`\Delta H _(r)^(\circ ) =`

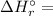
`\left [ 7* \Delta H _(f)^(\circ )\left (CO_(2)\right )+ 8* \Delta H _(f)^(\circ )\left (H_(2)O \right )\right ]`

`- \left [1* \Delta H _(f)^(\circ )\left (C_(7)H_(16)\right ) +11* \Delta H _(f)^(\circ )\left (O_(2) \right ) \right ]`

`=\left [ 7* \left (-393.5 kJ/mol \right )+ 8* \left (-286 kJ/mol \right )\right ]`

`-\left [1* \left (-187.8 kJ/mol \right ) +11* \left (0 kJ/mol \right ) \right ]`

⇒
`\Delta H _(r)^(\circ ) = \left [ \left (-2754.5 \right )+ \left (-2288 \right )\right ]\left -[ \left (-187.8 \right ) +\left (0 \right )\right ]`

⇒
`\Delta H _(r)^(\circ ) = \left [ -5042.5 ]\left -[ -187.8] = \left ( -4854.7kJ \right )`

To calculate the difference: ΔH-ΔE=Δ(PV)

We use the ideal gas equation: P.V = n.R.T

⇒ ΔH-ΔE=Δ(PV) = Δn.R.T

Given: Temperature:T = 298K, R = 8.314 J⋅K⁻¹⋅mol⁻¹

Δn = number of moles of gaseous products - number of moles of gaseous reactants = (7)- (11) = (-4)

⇒ ΔH-ΔE=Δ(PV) = Δn.R.T = (-4 mol) × (8.314 J⋅K⁻¹⋅mol⁻¹) × (298K) = 9910.288 J = 9.91 kJ (∵ 1 kJ = 1000J )