Question

Which sequences could be described by the recursive definition a_(n+1)=3*a_(n)-1

A. 2, 5, 14, 41, 122...
B. 2, 5, 8, 11, 14...
C. 2, 3, 5, 11, 29, 86...
D. 2,6,18,54,162...

Answer 1

B. 2, 5, 8, 11, 14...

Explanation:

Answer 2

And assuming that the first term of the sequence is 1,
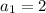`a_1 =2`, we can find the next values like this:

`a_2 = 3a_1 -1 = 3*2 -1 =5`

`a_3 = 3*a_2 -1 = 3*5 -1 =14`

`a_4 = 3*a_3 -1 = 3*14 -1 =41`

`a_5 = 3*a_4 -1 = 3*41 -1 =122`

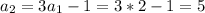
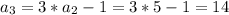
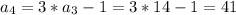
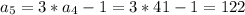
So then the sequence is given by: 2,5,14,41,122,... and the correct answet would be:

A. 2, 5, 14, 41, 122...

Explanation:

For this case we have a sequence defined by the following expression:

`a_(n+1)= 3 a_n -1`

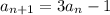
And assuming that the first term of the sequence is 1,
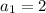`a_1 =2`, we can find the next values like this:

`a_2 = 3a_1 -1 = 3*2 -1 =5`

`a_3 = 3*a_2 -1 = 3*5 -1 =14`

`a_4 = 3*a_3 -1 = 3*14 -1 =41`

`a_5 = 3*a_4 -1 = 3*41 -1 =122`

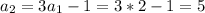
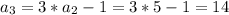
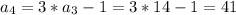
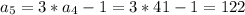
So then the sequence is given by: 2,5,14,41,122,... and the correct answet would be:

A. 2, 5, 14, 41, 122...