Question

A rocket accelerates by burning its onboard fuel, so its mass decreases with time. Suppose the initial mass of the rocket at liftoff (including its fuel) is m, the fuel is consumed at rate r, and the exhaust gases are ejected with constant velocity ve (relative to the rocket). A model for the velocity of the rocket at time t is given by the equation:

v(t)=−gt−velnm−rtm


Where g is the acceleration due to gravity and t is not too large?If g=9.8m/s2, m=29,000kg, r=170kg/s, and ve=2,900m/s.

What would the height of the rocket be one minute after liftoff?

Answer 1

Height of the rocket be one minute after liftoff is 40.1382 km.

Step-by-step explanation:

`v(t)=-gt-v_e* \ln (m-rt)/(m)`

v = velocity of rocket at time t

g = Acceleration due to gravity =
`9.8 m/s^2`

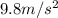
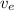`v_e` = Constant velocity relative to the rocket = 2,900m/s.

m = Initial mass of the rocket at liftoff = 29000 kg

r = Rate at which fuel is consumed = 170 kg/s

Velocity of the rocket after 1 minute of the liftoff =v

t = 1 minute = 60 seconds'

Substituting all the given values in in the given equation:

`v(60)=-9.8 m/s^2* 60 s-2,900m/s* \ln ((29,000 kg-170 kg/s* 60 s)/(2,9000 kg))`

`v(60) = 668.97 m/s`

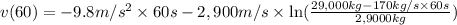
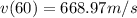
Height of the rocket = h

`Velocity=(Displacement)/(time)`

`668.97 m/s=(h)/(60 s)`

`h=668.97 m/s* 60 s=40,138.2 m = 40.1382 km`

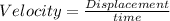
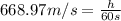
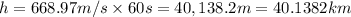
Height of the rocket be one minute after liftoff is 40.1382 km.