Step-by-step explanation:
It is known that the change in Gibb's free energy varies with temperature as follows.

=
![\Delta H(T_(f)) - \Delta C_(p,m) (T - T_(f)) - T[\Delta S(T_(f)) - \Delta C_(p,m) ln ((T)/(T_(f)))]](https://img.qammunity.org/2020/formulas/chemistry/high-school/2eytbrh8zzyhj03mdupa08qhy7jez0yype.png)
 (assumption)
(assumption)
=
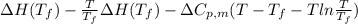
=
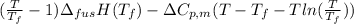
As, T =
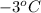 = (-3 + 273) = 270 K,
= (-3 + 273) = 270 K,
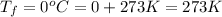 .
.
Therefore, calculate the change in Gibb's free energy as follows.

=

= -65.93 J/mol K + 0.62 J/mol K
= -65.31 J/mol K
Thus, we can conclude that Gibbs energy of freezing for the given reaction is -65.31 J/mol K.