Question

A playground merry-go-round has a mass of 50 kg and a diameter of 4.0 m. There are 4 children who want to ride on it. They have masses of 15 kg, 18 kg, 22 kg, and 25 kg. They start out on the edge of the merrygo-round but later move toward the center until they are halfway between the edge and the center.

A. Sketch the arrangement of the children on the merry-go-round when they are at the edge and halfway to the middle.
B. What is the total moment of inertia for both arrangements?
C. The children are standing at the edge when their parents get the ride turning at 0.21 radians/sec. What is their tangential velocity and the period of rotation?
D. While the ride rotates the children move to their positions halfway to the center. What is the angular velocity when they get to their new spots? Explain.

Answer 1

B) I1 = 1680 kg.m^2 I2 = 1120 kg.m^2

C) V = 0.84m/s T = 29.92s

D) ω2 = 0.315 rad/s

Step-by-step explanation:

The moment of inertia when they are standing on the edge:

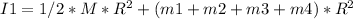`I1 = 1/2*M*R^2 + (m1+m2+m3+m4)*R^2` where M is the mass of the merry-go-round.

I1 = 1680 kg.m^2

The moment of inertia when they are standing half way to the center:

`I2 = 1/2*M*R^2 + (m1+m2+m3+m4)*(R/2)^2`

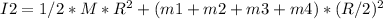
I2 = 1120 kg.m^2

The tangencial velocity is given by:

V = ω1*R = 0.84m/s

Period of rotation:

T = 2π / ω1 = 29.92s

Assuming that there is no friction and their parents are not pushing anymore, we can use conservation of the angular momentum to calculate the new angular velocity:

I1*ω1 = I2*ω2 Solving for ω2:

ω2 = I1*ω1 / I2 = 0.315 rad/s