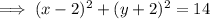Question

Center at (2, -2) and twice the area of the circle (x, -7)² + (y, -7)² =7​

Answer 1

`(x-2)^2+(y+2)^2=14`

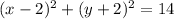
Explanation:

Equation of a circle

`(x-a)^2+(y-b)^2=r^2`

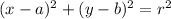
where:

• (a, b) is the center of the circle.
• r is the radius of the circle.

Given equation:

`(x-7)^2+(y-7)^2=7`

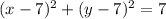
Therefore:

• center = (7, 7)
• radius = √7

Area of a circle

`\sf A=\pi r^2`

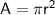
where:

• r is the radius.

Therefore, the area of a circle with radius √7 is:

`\implies \sf Area=\pi \left(√(7)\right)^2=7 \pi\:\:square\:units`

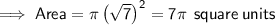
Therefore, a circle with twice the area would be:

`\implies \sf Area = 2 \cdot 7 \pi = 14 \pi \:\: square\:units`

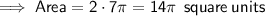
Therefore, its radius would be:

`\begin{aligned}\implies \sf \pi r^2 & = \sf14 \pi\\\sf r^2 & = \sf 14\\\sf r & = \sf √(14)\end{aligned}`

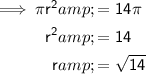
So the equation of a circle with a center at (2, -2) and a radius of √14 is:

`\implies (x-2)^2+(y-(-2))^2=\left(√(14)\right)^2`

`\implies (x-2)^2+(y+2)^2=14`