Question

What is the equation of the line in slope-intercept form?

Write your answer using integers, proper fractions, and improper fractions in
simplest form

Answer 1

The equation of the line in the slope-intercept form will be:

• y = -7x

Explanation:

The slope-intercept form of the line equation

y = mx+b

where

• m is the slope

• b is the y-intercept

From the attached graph, taking two points

• (0, 0)

• (-10, 70)

Finding the slope between (0, 0) and (-10, 70)

`\mathrm{Slope}=(y_2-y_1)/(x_2-x_1)`

`\left(x_1,\:y_1\right)=\left(0,\:0\right),\:\left(x_2,\:y_2\right)=\left(-10,\:70\right)`

`m=(70-0)/(-10-0)`

`m=-7`

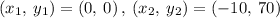
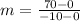
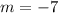
Determining the y-intercept:

We know that the value of y-intercept can be determined by setting x = 0, and determining the corresponding value of y.

From the graph, it is clear that:

at x = 0, y = 0

Thus, the y-intercept b = 0

Now, substituting m = -7 and b = 0 in the slope-intercept form

y = mx+b

y = -7x + 0

y = -7x

Therefore, the the equation of the line in slope-intercept form will be:

• y = -7x