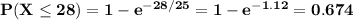Question

The random variable X is exponentially distributed, where X represents the time it takes for a person to choose a birthday gift. If X has an average value of 25 minutes, what is the probability that X is less than 28 minutes? (Do not round until the final step. Round your answer to 3 decimal places.)

Answer 1

0.674

Explanation:

If the random variable X is exponentially distributed and X has an average value of 25 minutes, then its probability density function (PDF) is

`\bf f(x)=(1)/(25)e^(-x/25)\;(x\geq 0)`

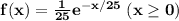
and its cumulative distribution function (CDF) is

`\bf P(X\leq t)=\int_(0)^(t) f(x)dx=1-e^(-t/25)`

So, the probability that X is less than 28 minutes is

`\bf P(X\leq 28)=1-e^(-28/25)=1-e^(-1.12)=0.674`