Question

The coordinates of the vertices of a triangle are P(- 5, 3), 0(7, - 2) , and R(10, - 1) . Find the length of the midsegment that is parallel to overline PQ .

Answer 1

6.5 units

Explanation:

The coordinates of the vertices of Δ PQR are P(-5,3), Q(7,-2) and R(10,-1).

So, coordinates of mid point of PR segment are
`[(-5+10)/(2), (3-1)/(2)]=(2.5,1)`

Again the coordinates of mid point of QR segment are
`[(7+10)/(2) ,(-2-1)/(2) ]=(8.5,-1.5)`

Therefore, the length of the mid segment that is parallel to over-line PQ will be
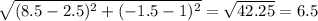`\sqrt{(8.5-2.5)^(2)+(-1.5-1)^(2)  } =√(42.25)= 6.5` units. ( Answer )