Question

I have tried to to write the inequality for this but not unsure of my answer,please help me. here it is........A college is currently accepting students that are both in-state and out-of-state. They plan to accept two times as many in-state students as out-of-state, and they only have space to accept 200 out-of-state students. Let x = the number of out-of-state students and y = the number in-state students.

I think the answer is x>0 and y>0

Answer 1

Answers:

`0 \le x \le 200`

`0 \le y \le 400`

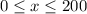
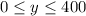
where x and y are integers

==================================================

Step-by-step explanation:

x = number of out-of-state students

y = number of in-state students

both x and y are integers (basically numbers that dont have a decimal portion)

Given fact 1: "They plan to accept two times as many in-state students as out-of-state"

Given fact 2: "they only have space to accept 200 out-of-state students"

Because of fact 1 above, we can say y = 2*x or y = 2x. Whatever the x value is, we multiply by 2 to get the y value.

Based on fact 2, we know that x cannot exceed 200. Put another way, the largest x can get is 200. So we write
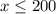`x \le 200`. At the same time, x cannot be less than 0, so we also say
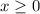`x \ge 0` which is the same as
`0 \le x`

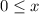
Combine
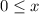`0 \le x` and
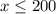`x \le 200` to form the compound inequality
`0 \le x \le 200`

------------

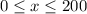
From here, multiply all three sides by 2 to get the following

`0 \le x \le 200`

`2*0 \le 2*x \le 2*200`

`0 \le 2x \le 400`

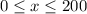
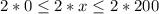
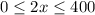
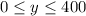`0 \le y \le 400` note the replacement of 2x with y (since y = 2x)

which shows that the college will accept up to 400 new in-state students.