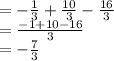Question

Find $a+b+c$ if the graph of the equation $y=ax^2+bx+c$ is a parabola with vertex $(5,3)$, vertical axis of symmetry, and contains the point $(2,0)$.

Answer 1

`a+b+c=-(7)/(3)`

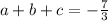
Explanation:

Given:

The equation of the parabola with vertical axis of symmetry is given as:

`y=ax^2+bx+c`

Vertex of the parabola is,
`(h,k)=(5,3)`

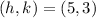
Point on a parabola is (2,0).

The
`x` co-ordinate of the vertex is given as:

`h=-(b)/(2a)\\5=-(b)/(2a)\\5* 2a=-b\\10a=-b\\b=-10a----1`

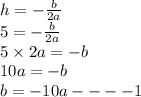
Now, plug in the point (2,0) in the parabolic equation. This gives,

`0=a(2)^2+b(2)+c\\0=4a+2(-10a)+c\\0=4a-20a+c\\c=20a-4a=16a------ 2`

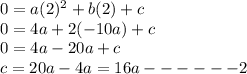
Now, as vertex lies on the parabola, plug in (5,3) in the parabolic equation. This gives,

`3=a(5)^2+b(5)+c\\3=25a+5b+c\\\textrm{But, b= -10a, c= 16a}\\3=25a+5(-10a)+16a\\3=25a-50a+16a\\3=-9a\\a=-(3)/(9)=-(1)/(3)----3`

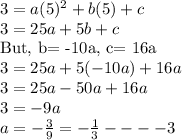
So,

`b=-10a=-10* -(1)/(3)=(10)/(3)\\c=16a=16* -(1)/(3)=-(16)/(3)`

Therefore, the sum of
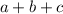`a+b+c` is:

`=-(1)/(3)+(10)/(3)-(16)/(3)\\=(-1+10-16)/(3)\\=-(7)/(3)`