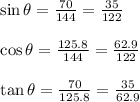Question

How do I solve a given right triangle to find Cos, Sin, and Tan. How do I solve for a missing adjacent side? (For Example: Imagine a right triangle with A, B, and C. 70 inches = opposite

12 feet = hypotenuse
x = adjacent. There is no given degree.

Answer 1

The steps to find cos, sin, and tan and missing adjacent side of a given right angle triangle is explained.

Solution:

Given, a right triangle with A, B, and C.

Opposite side = 70 inches

Hypotenuse = 12 feet = 12
`*` 12 inches = 144 inches

Adjacent side = "x" inches.

We are not given angle, so we have to use the hypotenuse theorem

Hypotenuse theorem means square of the length of the hypotenuse is equal to the sum of squares of the lengths of other two sides of the right-angled triangle.

`\text { hypotenuse }^(2)=(\text { opposite side })^(2)+(\text { adjacent side })^(2)`

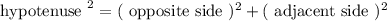
Substituting the values we get,

`\begin{array}{l}{\rightarrow 144^(2)=70^(2)+x^(2)} \\\\ {\rightarrow x^(2)=20736-4900} \\\\ {\rightarrow x^(2)=15836} \\\\ {\rightarrow x=√(15836)} \\\\ {\rightarrow x=125.841}\end{array}`

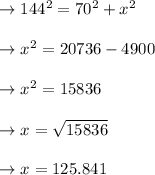
So, the adjacent side value is 125.8 inches approximately.

Hence the steps to find adjacent side is shown above

Now let us find cos, sin and tan

`\begin{aligned} \sin \theta &=\frac{\text {opposite side}}{\text {hypotenuse}} \\\\ \cos \theta &=\frac{\text {adjacent side}}{\text {hypotenuse}} \\\\ \tan \theta &=\frac{\text {opposite side}}{\text {adjacent side}} \end{aligned}`

By substituting the required values, we can find cos, sin and tan

`\begin{array}{l}{\sin \theta=(70)/(144)=(35)/(122)} \\\\ {\cos \theta=(125.8)/(144)=(62.9)/(122)} \\\\ {\tan \theta=(70)/(125.8)=(35)/(62.9)}\end{array}`