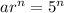Explanation:
Geometric progression, is a sequence of numbers where each term after the first is found by multiplying the previous one by a fixed, non-zero number called the common ratio.
The first term of the Geometric progression is
 and common ratio is
and common ratio is
 .
.
The series will look like
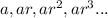
With
 and
and
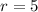 ,
,
we get
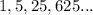
This is the given sequence.
Any term can be calculated by