Answer:
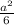 square units.
square units.
Explanation:
The given curve is √x + √y = √a ......... (1)
Now, the curve intersects the x-axis at (a,0) point and the y-axis at (0,a) point.
Therefore, the are limited by equation (1) and the coordinate axes will be
=
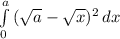
=
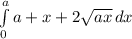
=
![[ax + (x^(2) )/(2)+ 2√(a)\frac{x^{(3)/(2) } }{(3)/(2) } ]_(0) ^(a)](https://img.qammunity.org/2020/formulas/mathematics/middle-school/zbo69k9axw6emkkg61pblyj5j0dlp25wk7.png)
=

=
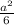 square units. (Answer)
square units. (Answer)