Answer:
Normal force acting on the woman is 629.85 N.
Step-by-step explanation:
Given:
Mass of the woman is,
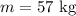
Net upward acceleration is,
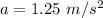
Acceleration due to gravity,

Let the normal force acting upward be
 newtons.
newtons.
Therefore, net force in the upward direction is given as:
Net force = Upward force - Downward force.
Downward force acting on the woman is her weight which is equal to
 .
.
Therefore, Net force =
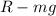
Now, as per Newton's second law of motion,
Net force,
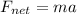
So,

Plug in 57 kg for
 , 9.8 m/s² for
, 9.8 m/s² for
 , and 1.25 m/s² for
, and 1.25 m/s² for
 . Solve for
. Solve for
 . This gives,
. This gives,

Therefore, the normal force acting on her is 629.85 N.