Question

Suppose f(x)=x^2 and g(x)=(3x)^2 which statement best compares the graph of g(x) with the graph of f(x)?

A.the graph of g(x) is vertically stretched by a factor of 3

B. The graph of g(x) is shifted to the right

C.the graph of g(x) is horizontally compressed by a factor of 3

D.the graph g(x) is horizontally stretched by a factor of 3

Answer 1

C. The graph g(x) is horizontally compressed by a factor of 3.

Explanation:

Given:

`f(x)=x^(2),g(x)=(3x)^(2)`

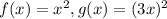
Here, the graph of
`g(x)` is a transformation of the parent function
`f(x)`.

In order to transform
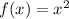`f(x)=x^(2)` to
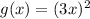`g(x)=(3x)^(2)`, we need to perform the following transformation:

`f(x)\rightarrow f(3x)\\x^2\rightarrow (3x)^2`

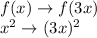
As per the transformation rules, if a positive number greater than 1 is multiplied to
`x` of the function, then the graph of the function compresses in the horizontal direction.

As 3 is multiplied to
`x` of
`f(x)`, therefore, the graph of
`g(x)` is a horizontal compression by a factor of 3.