Question

The hypotenuse of right triangle is 122 meters long. The difference between the other two sides is 98 meters. Find the missing sides. Use exact values.

Answer 1

The length of the Base = 22 meters

Length of the perpendicular is = 120 meters

Explanation:

The length of the hypotenuse = 122 m

Let base side of the triangle = k meters

So, the perpendicular side of the triangle is = 98 + k

Now, by PYTHAGORAS THEOREM , in a right angled triangle:

`(BASE)^(2) + (PERPENDICULAR) ^(2)  =  (HYPOTENUSE)^(2)`

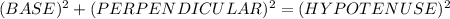
⇒ Here,
`(k)^(2)   + ( k+ 98)^2  =( 122)^2`

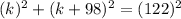
Also, by Algebraic Identity:
`(a+b)^(2)   = a^(2) + b ^(2) + 2ab  \implies (k+98)^(2)   = k^(2) + (98) ^(2) + 2k(98)`

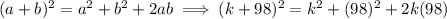
or,
`(k)^(2)   +  k^(2) + (98) ^(2) + 2k(98)  =( 122)^2`

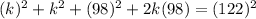
or,
`2k^(2)  + 9604 + 196k = 14884\\\implies  k^(2) + 98k -2640 = 0`

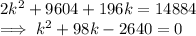
Solving the equation:
`k^(2) +120k - 22k - 2640 = 0 \implies k(k+120)-22(k+120) = 0`

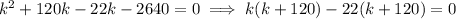
⇒ (k+120)(k-22) = 0 , or (k+120) = 0 , or (k-22) = 0

or, either k = -120 , or k = 22

As k is the length of the side, so k ≠ - 120

Hence, the length of the base = k = 22 meters

and the length of the perpendicular is k + 98 = 120 meters