Question

It is a hot day in july. The temp in the morning is 5 Celcius and the pressure indicator on the tak of Nitrogen measures 861mmHg. Durin the hottes part of the day the temp reaches a high of 28 Celcius. What is the new pressure readin on the indicator?​

Answer 1

`\large \boxed{\text{932 mmHg}}`

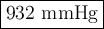
Step-by-step explanation:

The volume and amount are constant, so we can use Gay-Lussac’s Law:

At constant volume, the pressure exerted by a gas is directly proportional to its temperature.

`(p_(1))/(T_(1)) = (p_(2))/(T_(2))`

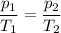
Data:

p₁ = 861 mmHg; T₁ = 5 °C

p₂ = ?; T₂ = 28 °C

Calculations:

(a) Convert the temperatures to kelvins

T₁ = ( 5 + 273.15) K = 278.15 K

T₂ = (28 + 273.15) K = 301.15 K

(b) Calculate the pressure

`\begin{array}{rcl}(861)/(278.15) & = & (p_(2))/(301.15)\\\\3.095 & = & (p_(2))/(301.15)\\\\3.095*301.15&=&p_(2)\\p_(2) & = & \mathbf{932}\end{array}\\\text{The new pressure reading will be $\large \boxed{\textbf{932 mmHg}}$}`