Answer:
The first 3 terms in the expansion of
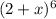 , in ascending power of x are,
, in ascending power of x are,
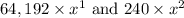
coefficient of
 in the expansion of
in the expansion of
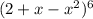 = (240 - 192) = 48
= (240 - 192) = 48
Explanation:
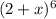
=
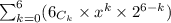
=
 + terms involving higher powers of x
+ terms involving higher powers of x
=
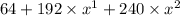 + terms involving higher powers of x
+ terms involving higher powers of x
so, the first 3 terms in the expansion of
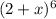 , in ascending power of x are,
, in ascending power of x are,
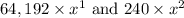
Again,
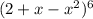
=

Now, by inspection,
the term
 comes from k =5 and k = 6
comes from k =5 and k = 6
for k = 5, the coefficient of
 is ,
is ,
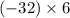 = -192
= -192
for k = 6 , the coefficient of
 is,
is,
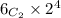 = 240
= 240
so, coefficient of
 in the final expression = (240 - 192) = 48
in the final expression = (240 - 192) = 48