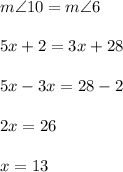Answer:
40. Alternate exterior angles
41. 108°
42. x = 4
43. x = 13
Explanation:
40. Given l || m, line n is transversal (intersects lines m and l), then angles 10 and 6 are alternate exterior angles.
41. Given l || m, line n is transversal (intersects lines m and l), then angles 2 and 3 are same side interior angles. Same side interior angles are supplementray (add up to 180°), so if m∠2=72°, then
m∠3=180°-72°=108°
42. Given l || m, line n is transversal (intersects lines m and l), then angles 10 and 6 are alternate interior angles. Alternate interior angles are congruent, so
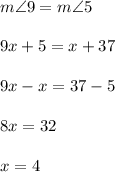
43. If alternate exterior angles 10 and 6 are congruent, then lines l and m are parallel. Find the value of x for which angles 10 and 6 are congruent.