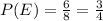Question

Use the game spinner for questions 1-4. In your final answer, include all necessary calculations.

Find the probability that the spinner will land on an even number.
Find the probability that the spinner will land on an odd number.
Find the probability that the spinner will not land on 2 or 3.
Find the probability that the spinner will not land on a multiple of 3.

Answer 1

Step-byWill the spinner land on a even number P = 1/2 for a even number Odd number 1/2

Spinner will not hit a 2 or a 3 = 3/4 Spinner hit a multple of 3 = 3/4

8 numbers 1-8 P(E) Favorable outcomes Total outcomes

Odds of getting a even number 2,4,6,8 P(E) 4/8 = 1/2 Land on a odd number 1,3,5,7 P(E) 4/8 = 1/2 Not hit a 2 or 3

1,4,5,6,7,8, P(E) = 6/8 = 3/4 Not hit a multiple of 3 1,2,4,5,6,7,8 P(t)b= 6/8 = 3/4-step explanation:

Answer 2

P (Even number) = 1/2

P(spinner will land on an odd number) = 1/2

P(spinner will not land on 2 or 3) = 3/4

P(spinner will not land on a multiple of 3) = 3/4

Explanation:

Here, while spinning the spinner total possible outcomes

are 8 = {1,2,3,4,5,6,7,8}

Now,
`\textrm{P(E)}  = \frac{\textrm{Number of favorable outcomes }}{\textrm{Total numberof outcomes}}`

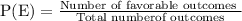
a) E: Probability of getting even number

Favorable outcomes are {2,4,6,8}

Hence,
`P(E) = (4)/(8)  = (1)/(2)`

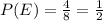
b)E: Probability that the spinner will land on an odd number.

Favorable outcomes are {1,3,5,7}

Hence,
`P(E) = (4)/(8)  = (1)/(2)`

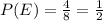
c) E: Probability that the spinner will not land on 2 or 3

Favorable outcomes are {1, 4,5,6,7,8}

Hence,
`P(E) = (6)/(8)  = (3)/(4)`

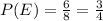
d) E: Probability that the spinner will not land on a multiple of 3

Favorable outcomes are {1,2,4,5,7,8}

Hence,
`P(E) = (6)/(8)  = (3)/(4)`