Answer:
The required probability is 0.5
Explanation:
Consider the provided information.
A manager of an apartment store reports that the time of a customer on the second floor must wait for the elevator has a uniform distribution ranging from 2 to 4 minutes. it takes the elevator 30 seconds to go from floor to floor.
Let x denotes the waiting time.
It is given that waiting time is uniformly distributed from 2 to 4.
It is given that it takes 30 seconds to go from floor to floor.
Convert 30 seconds into minutes:
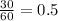 min
min
Time to reach first floor is uniformly distributed:
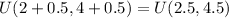
We need to determine the probability that a hurried customer can reach the first floor in less than 3.5 minutes after pushing the elevator button on the second floor."
So we need to find
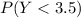

Hence, the required probability is 0.5