Answer:
The area of Rectangle with given vertices is 6 unit ²
Explanation:
Given points of vertices of rectangle as :
A = ( - 4, 0)
B = ( - 3 , 1)
C = ( 0 , - 2)
D = ( - 1 , - 3)
Now the measure of side AB =
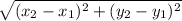
So, AB =
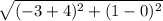
AB =
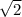 unit
unit
The measure of side BC =
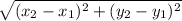
BC =
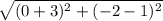
BC = 3
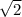 unit
unit
The measure of side CD =
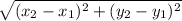
CD =
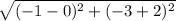
CD =
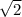 unit
unit
The measure of side DA =
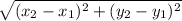
DA =
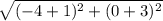
DA = 3
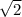 unit
unit
So, the measure of side AB = The measure of side CD =
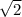 unit
unit
And The measure of side BC = The measure of side DA = 3
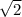 unit
unit
So, Let Length = AB = CD
And Width = BC = DA
∴ The area of Rectangle = Length × Width unit²
Or, The area of Rectangle = AB × BC
So, The area of Rectangle =
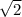 unit × 3
unit × 3
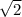 unit
unit
∴ The area of Rectangle = 6 unit ²
Hence The area of Rectangle with given vertices is 6 unit ² Answer