Answer:
perimeter = 32
Explanation:
To find the perimeter of a polygon with the following vertices at; (3,2),(3,9),(7,12),(11,9), and (11,2), we will need to find the distance around the polygon.
Let A,B,C,D,E be the vertices of the polygon.
That is A(3,2), B(3,9), C(7,12), D(11,9), and E(11,2)
Then we will find the distance AB, BC, CD, DE and EA.
So to do this, we will simply apply our distance formula;
d = √ (
 )² + (
)² + (
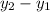 )²
)²
We can now proceed;
A(3,2) B(3,9)
|AB| = √ (
 )² + (
)² + (
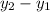 )²
)²
=√(3-3)² + (9-2)²
=√0² + 7²
=√7²
=√49
=7
|AB| = 7
Then, B(3,9) C(7,12)
|BC| = √ (
 )² + (
)² + (
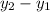 )²
)²
= √(7-3)² + (12-9)²
=√4² + 3²
=√16 +9
=√25
=5
|BC| =5
Then, C(7,12) D(11,9)
|CD| = √ (
 )² + (
)² + (
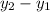 )²
)²
=√(11-7)² + (9-12)²
=√4² + 3²
=√16 + 9
=√25
=5
|CD| = 5
Then, D(11,9) E(11,2)
|DE| = √ (
 )² + (
)² + (
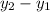 )²
)²
=√(11-11)² + (2-9)²
=√0² + 7²
=√49
=7
|DE|=7
Then, E(11,2) A(3,2)
|EA| = √ (
 )² + (
)² + (
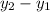 )²
)²
=√(3-11)² - (2-2)²
=√(-8)² + 0²
=√64
=8
|EA| = 8
Perimeter = |AB| +|BC| + |CD| + |DE| + |EA|
=7 + 5 + 5 + 7 + 8
=32
Therefore, the perimeter of the polygon is 32