Question

convenient source of gamma rays for radiation chemistry research is 60Co, which decays to give a beta particle, gamma rays and 60Ni. The half-life for the decay is 1.9 x 103 days. What is the rate constant for the decay process? How long will it take for a sample of 60Co to decay to 1/8th of its original concentration.

Answer 1

Rate constant:
`\lambda= 3.65 \cdot 10^(-04) d^(-1)`

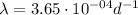
Time to deacy to 1/8 of its original cocentration:
`t = 5697.1 d = 15.6 years`

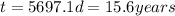
Explanation:

To find the rate constant for the decay process, we use the next equation:

`t_{(1)/(2)}=(Ln(2))/(\lambda)`

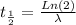
where λ: constant for the decay process, and
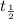`t_{(1)/(2)}`: half-life for the decay

`\lambda=\frac{Ln(2)}{t_{(1)/(2)}}`

`\lambda=(Ln(2))/(1.9\cdot 10^(3))`

`\lambda= 3.65 \cdot 10^(-04) d^(-1)`

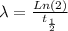
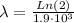
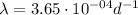
Now, to calculate the time for a sample of 60Co to decay to 1/8th of its original concentration, we use the exponential decay equation:

`N_((t))=N_(0) \cdot e^(-\lambda \cdot t)`

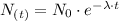
where
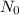`N_(0)` : initial quantity of the 60Co and
`N_((t))` : is the quantity has not yet decayed after a time t.

`(N_(0))/(8)=N_(0) \cdot e^(-\lambda \cdot t)`

`Ln((1)/(8))=-\lambda \cdot t`

`t = -(Ln((1)/(8)))/(\lambda)`

`t = -(Ln((1)/(8)))/(3.65 \cdot 10^(-04))`

`t = 5697.1 d = 15.6 years`

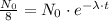
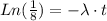
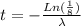
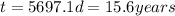
Have a nice day!