Answer:
The force acting on the shaft is 1324.75 N
Step-by-step explanation:
Given that,
Cross sectional area of shaft
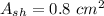
Gas pressure
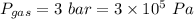
Total mass M=24.5+0.5=25 kg
Diameter of piston, d=10 cm
We need to calculate the cross section area of piston
Using formula of area
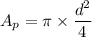
Put the value into the formula
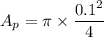
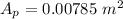
We need to calculate the weight of the piston and shaft
Using formula of weight
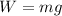
Put the value into the formula
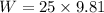
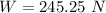
We need to calculate the force due to gas pressure
Using formula of force
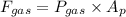
Put the value into the formula
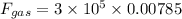
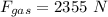
We need to calculate the force due to atmospheric pressure,
Using formula of force
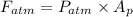
Put the value into the formula
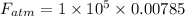

We need to calculate the force acting on the shaft
from free body diagram
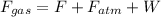
Put the value into the formula
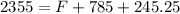

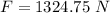
Hence, The force acting on the shaft is 1324.75 N