Question

A car company has found that there is a linear relationship between the amount of money it spends on advertising and the number of cars it sells. When it spent 60,000 dollars on advertising, it sold 440 cars. Moreover, for each additional 10,000 dollars spent, they sell 40 more cars.

A. If a car company invested 90,000 dollars in advertising, then how many cars did it sell?
B. If a car company sold 800 cars, then how much did it invest in advertising?
C. Write an equation in y=mx +b form for the number of cars sold as a function of the amount of money spent on advertising. Give units and real world meaning for m and b.
D. Write an equation in y=mx + b form for the amount of money spent on advertising as a function of the number of cars sold. Give units and real world meaning for m and b.

Answer 1

a) It is expected to sell 560 cars.

b) The total amount invested is $145,000.

c)
`y=0.004x+200`

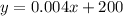
m is the slope of the linear function, and represents the additional amount of cars it will sell due to an additional dollar invested in advertising. Its units of m is [cars/dollar].

b is the y-intercept and represent the amount of cars the company would sell if there is 0 dollars invested in advertising. It may or not be a representative point in the real world (it depends on how accurate is the linear function and the range where it is valid). The unit of b is [cars].

Explanation:

a) If the company invest $90,000, that is 3 times $10,000 plus the originals $60,000. Then, it is expected to sell 560 cars.

`440+3*40=440+120=560`

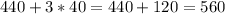
b) If the company sold 800 cars, we have 440 cars that corresponds to the original $60,000 and (800-440)=360 cars that correspond to the additional invest.

If an additional 40 cars are sold by an additional $10,000 invest, 340 cars are sold by 340*10,000/40= $85,000.

Then the total amount invested is 60,000+85,000=$145,000.

c) We can estimate the parameters m and b of the equation taking into account one known point ($60,000 corresponds to 440 sold cars) and the known variation (40 sold cars for every $10,000 invested).

`m=\frac {\Delta y} {\Delta x }=(40)/(10,000)=0.004 \, (cars)/(dollar)`

Then we can use the known point to estimate b:

`b=y-mx=440-(0.004)*60000=440-240=200 \, cars`

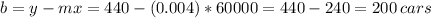
The equation is then

`y=0.004x+200`

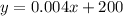
m is the slope of the linear function, and represents the additional amount of cars it will sell due to an additional dollar invested in advertising. Its units of m is [cars/dollar].

b is the y-intercept and represent the amount of cars the company would sell if there is 0 dollars invested in advertising. It may or not be a representative point in the real world (it depends on how accurate is the linear function and the range where it is valid). The unit of b is [cars].