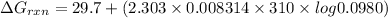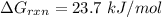Question

Consider the malate dehydrogenase reaction from the citric acid cycle. Given the following concentrations, calculate the free energy change for this reaction at 37.0 °C (310 K). ΔG°\' for the reaction is 29.7 kJ/mol. Assume that the reaction occurs at pH 7. [malate] = 1.13 mM [oxaloacetate] = 0.270 mM [NAD ] = 390 mM [NADH] = 160 mM

Answer 1

`\Delta G_(rxn)=23.7\ kJ/mol`

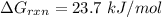
Step-by-step explanation:

According to the reaction,

`Malate + NAD^+\rightleftharpoons Oxaloacetate + NADH`

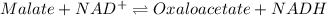
The expression for the equilibrium constant is:-

`K =\frac {[oxaloacetate][NADH]}{[malate][NAD^+]}`

Given:-

[malate] = 1.13 mM

[oxaloacetate] = 0.270 mM

`[NAD^+]` = 390 mM

[NADH] = 160 mM

Thus,

`K = ((0.270)(160))/((1.13)(390)) = 0.0980`

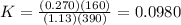
The expression for calculation of free energy change is shown below as:-

`\Delta G_(rxn)= \Delta G^0_(rxn) + 2.303RT* log\ K`

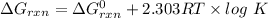
Where, R is gas constant, 8.314 J/K.mol

T is the temperature in Kelvins

So, Given:-
`\Delta G^0_(rxn)=29.7\ kJ/mol`

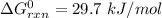
T = 310 K

Thus,

`\Delta G_(rxn)=29.7 + (2.303* 0.008314* 310* log 0.0980)`

`\Delta G_(rxn)=23.7\ kJ/mol`