Question

A ball is thrown in the air from the top of a building. Its height, in meters above ground, as a function of time, in seconds, is given by h(t)=−4.9x2+19.6x+24.How long does does it take for the ball to reach its maximum height? What is the maximum height of the ball?(Round your answer to three decimal places)

Answer 1

It would take 2 second to reach its maximum height.

The maximum height of the ball is 43.6 meters above the ground.

Explanation:

Consider the provided function.

`h(x)=-4.9x^2+19.6x+24`

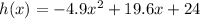
The above function's graph is a downward parabola and the maximum of the downward parabola is at its vertex.

We can find the x coordinate of the function using the formula:
`(-b)/(2a)`

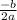
Substitute a=-4.9 and b=19.6 in
`(-b)/(2a)`

`x=(-19.6)/(2(-4.9))`

`x=(19.6)/(9.8)`

`x=2}`

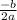
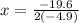
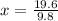
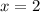
Hence, it would take 2 second to reach its maximum height.

Substitute x=2 in above formula.

`h(2)=-4.9(2)^2+19.6(2)+24`

`h(2)=-19.6+39.2+24`

`h(2)=43.6`

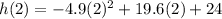
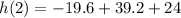
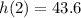
Hence, the maximum height of the ball is 43.6 meters above the ground.