Question

Suppose researchers are concerned about the rate of residents reporting no access to health insurance in a particular community. Suppose national statistics indicate that 24% of residents are living without health insurance. Assume the researchers sample a group of 10 households.a. What is the expected number of households that will have no insurance?b. What is the standard deviation?

Answer 1

a) The expected number of households that will have no insurance is 2.4.

b) The standard deviation is 1.3505.

Explanation:

For each resident, there are only two possible outcomes. Either they have health insurance, of they do not. This means that we can solve this problem using concepts of the binomial probability distribution.

Binomial probability distribution

Probability of exactly x sucesses on n repeated trials, with p probability.

The expected number of successes is given by:

`E(X) = np`

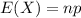
The standard deviation is given by:

`√(Var(X)) = √(np(1-p))`

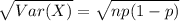
In this problem, we have that:

A group of 10 households, so
`n = 10`.

24% of residents are living without health insurance, so
`p = 0.24`.

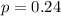a. What is the expected number of households that will have no insurance?

`E(X) = np = 10*0.24 = 2.4`

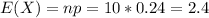
The expected number of households that will have no insurance is 2.4.

b. What is the standard deviation?

`√(Var(X)) = √(np(1-p) = √(10*0.24*0.76) = 1.3505`

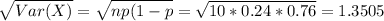
The standard deviation is 1.3505.