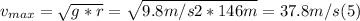Question

The same car now travels on a straight track and goes over a hill with radius 146 m at the top. What is the maximum speed that the car can go over the hill without leaving

Answer 1

v = 37.8 m/s

Step-by-step explanation:

• When at the top of the hill, the only force that keeps the car in the circular trajectory, is the centripetal force.
• This force is not a new force, is just the net force aiming to the center of the circle.
• In this case, is just the difference between the normal force (always perpendicular to the surface, pointing upward) and the force that gravity exerts on the car (which is known as the weight), pointing downward.
• So, we can write the following expression:

`F_(cent) = F_(g) - F_(n) (1)`

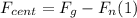
• It can be showed that the centripetal force is related to the speed by the following expression:

• 
  `F_(cent) = m*(v^(2))/(r) (2)`
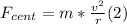
• Replacing (2) in (1), and solving for Fn, we get:
• 
  `F_(n) = F_(g) - m*(v^(2))/(r) (3)`
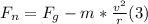
• Now, we need to find the value of v that makes Fn, exactly zero, because at a speed greater than this, the car will not be on track anymore.
• So we can write the following equation:
• 
  `m*(v^(2))/(r) = F_(g) (4)`
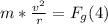
• Replacing Fg by its value, simplifying, and solving for v, we get:

`v_(max) = √(g*r) =√(9.8 m/s2*146 m) = 37.8 m/s (5)`